队列的顺序存储结构

队列的顺序存储

队列的顺序实现是指分配一块连续的存储单元存放队列中的元素，并附设两个指针：队首指针 front 指向队首元素，队尾指针 rear 指向队尾元素的下一个位置。

不同教材对 front 和 rear 的定义可能不同，例如，可以让 rear 指向队尾元素、front 指向队首元素。对于不同的定义，出入队的操作是不同的，本节后面有一些相关的习题，读者可以结合习题思考。

队列的顺序存储类型可描述为：

#define MaxSize 50  //定义队列中元素的最大个数
typedef struct {    //用数组存放队列元素
    ElemType data[MaxSize];  //队首指针和队尾指针
    int front, rear;
} SqQueue;

初始时：Q.front = Q.rear = 0
入队操作：队不满时，先送值到队尾元素，再将队尾指针加 1 。
出队操作：队不空时，先取队首元素值，再将队首指针加 1 。

图示为队列的初始状态，有 Q.front == Q.rear == 0 成立，该条件可以作为队列判空的条件。

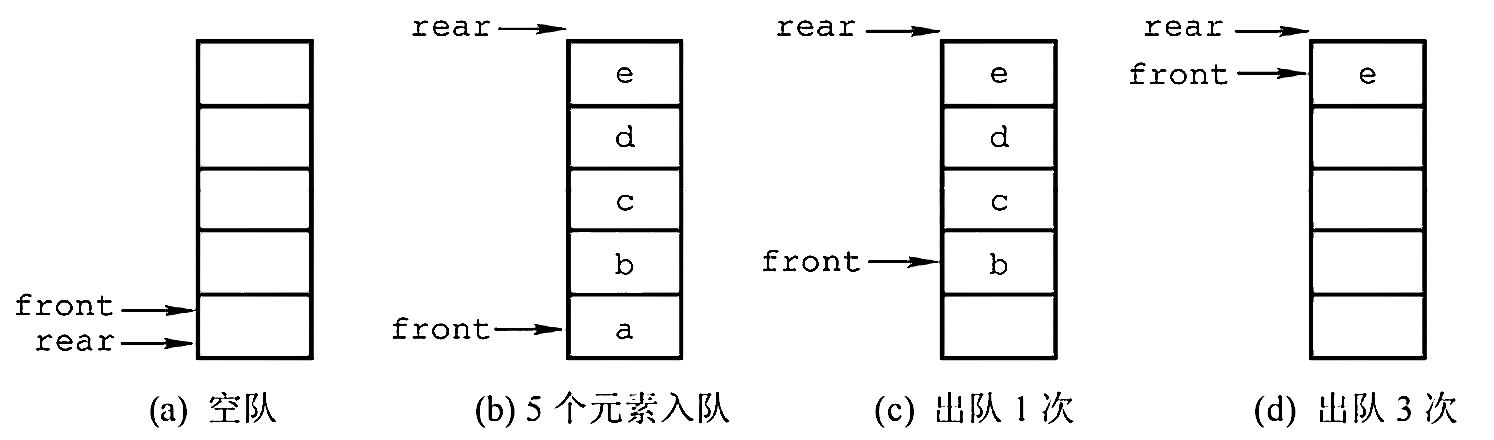
但能否用 Q.rear == MaxSize 作为队列满的条件呢？显然不能，图(d) 中，队列中仅有一个元素，但仍满足该条件。这时入队出现"上溢出"，但这种溢出并不是真正的溢出，在 data 数组中依然存在可以存放元素的空位置，所以是一种"假溢出"。

循环队列

上面指出了顺序队列"假溢出"的问题，这里引出循环队列的概念。将顺序队列臆造为一个环状的空间，即把存储队列元素的表从逻辑上视为一个环，称为循环队列。当队首指针 Q.front=MaxSize-1 后，再前进一个位置就自动到 0，这可以利用除法取模运算（%）来实现。

初始时：Q.front = Q.rear = 0
队首指针进1：Q.front = (Q.front + 1) % MaxSize
队尾指针进1：Q.rear = (Q.rear + 1) % MaxSize
队列长度：(Q.rear + MaxSize - Q.front) % MaxSize
出入队时：指针都按顺时针方向进1（如图所示）。

那么，循环队列队空和队满的判断条件是什么呢？显然，队空的条件是 Q.front == Q.rear 。若入队元素的速度快于出队元素的速度，则队尾指针很快就会赶上队首指针，如图(d1) 所示，此时可以看出队满时也有 Q.front == Q.rear 。循环队列出入队示意图如图所示。

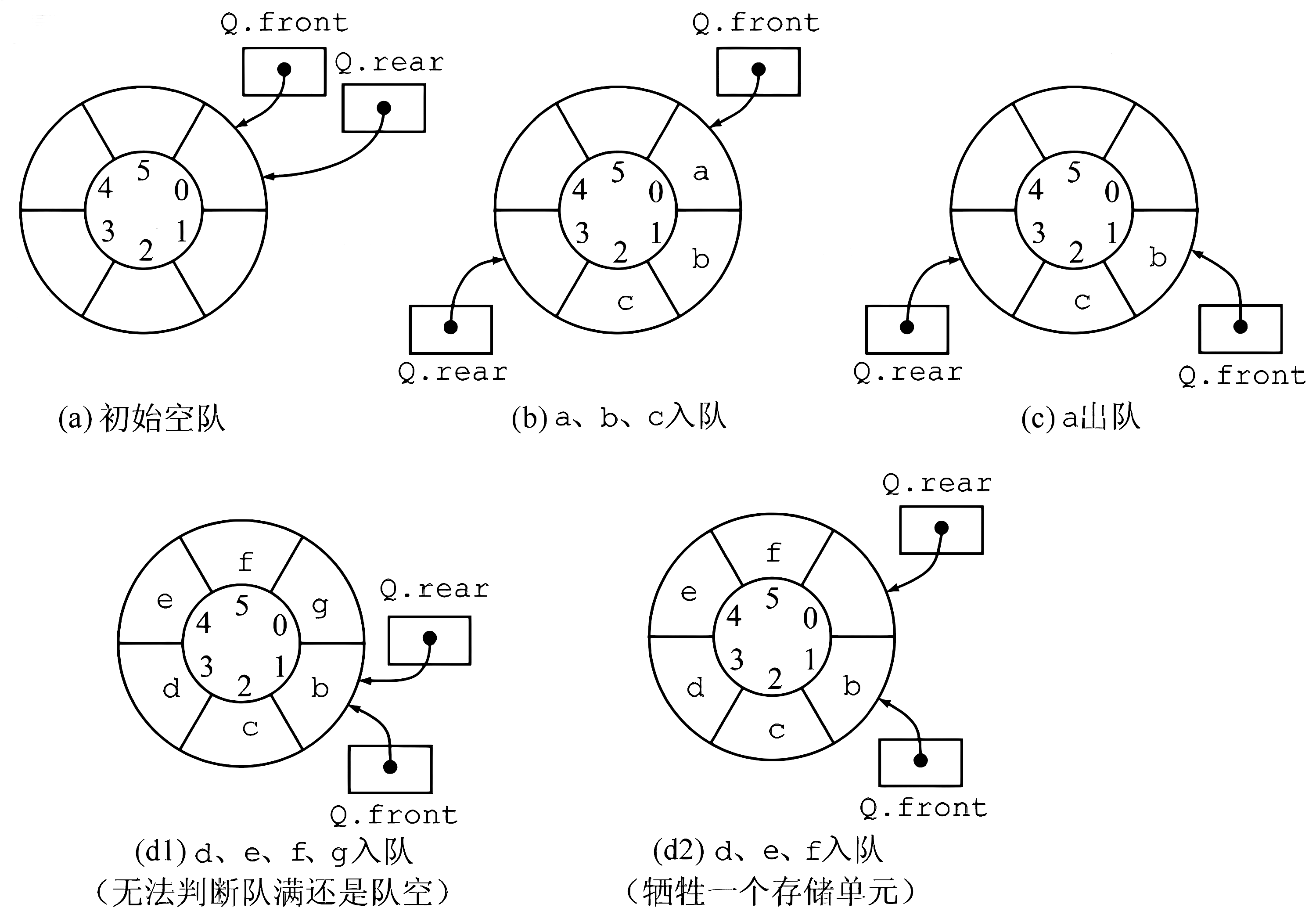
为了区分是队空还是队满的情况，有三种处理方式：

1）牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是一种较为普遍的做法，约定以"队首指针在队尾指针的下一位置作为队满的标志"，如图(d2) 所示。

队满条件：(Q.rear + 1) % MaxSize == Q.front
队空条件：Q.front == Q.rear
队列中元素的个数：(Q.rear - Q.front + MaxSize) % MaxSize

2）类型中增设 size 数据成员，表示元素个数。若删除成功，则 size 减 1 ，若插入成功，则 size 加 1，队空时 Q.size==0 ；队满时 Q.size==MaxSize ，两种情况都有 Q.front == Q.rear 。

3）类型中增设 tag 数据成员，以区分是队满还是队空。删除成功置 tag=0，若导致 Q.front == Q.rear ，则为队空；插入成功置 tag=1，若导致 Q.front == Q.rear ，则为队满。

循环队列的操作

初始化

void InitQueue(SqQueue &Q) {
    Q.rear = Q.front = 0; //初始化队首、队尾指针
}

判队空

bool isEmpty(SqQueue Q) {
    if (Q.front == Q.rear) //队空条件
        return true;
    return false;
}

入队

bool EnQueue(SqQueue &Q, ElemType x) {
    if ((Q.rear + 1) % MaxSize == Q.front) {
        return false;
    }
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1) % MaxSize;
    return true;
}

出队

bool DeQueue(SqQueue &Q, ElemType &x) {
    if (Q.front == Q.rear) {
        return false;
    }
    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}

队列的顺序存储结构 ​