第一章 题型梳理与强化

1 函数的基本性质及常见函数

题型1 函数与原函数间奇偶性、周期性关系

1. 导函数的奇偶性、周期性性质

（1）若函数 $f(x)$ 为可导的奇函数，则 $f^{\prime }(x)$ 为偶函数；

（2）若函数 $f(x)$ 为可导的偶函数，则 $f^{\prime }(x)$ 为奇函数；

（3）若函数 $f(x)$ 是以 $T$ 为周期的可导函数，则 $f^{\prime }(x)$ 也是以 $T$ 为周期的周期函数。

【注】连续的奇函数的所有原函数都是偶函数；但是，连续的偶函数的原函数中仅有一个原函数是奇函数。

---

2. 变上限函数与原函数之间的关系

若 $f(x)$ 连续，则 $F(x)=\begin{array}{r}{\int }_a^{x}f(t)\mathrm{d}t\end{array}$ 可导，且 $F^{\prime }(x)=f(x)$；

【注】若 $f(x)$ 连续，则 $F(x)=\begin{array}{r}{\int }_a^{x}f(t)\mathrm{d}t\end{array}$ 是 $f(x)$ 的一个原函数。

---

3. 变上限函数的奇偶性、周期性性质

设 $f(x)$ 连续，对于 $F(x)=\begin{array}{r}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$ 有：

（1）若 $f(x)$ 为奇函数，则 $F(x)=\begin{array}{r}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$ 为偶函数；

（2）若 $f(x)$ 为偶函数，则 $F(x)=\begin{array}{r}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$ 为奇函数；

（3）若 $f(x)$ 是以 $T$ 为周期的周期函数，且 $\begin{array}{r}{\int }_0^{T}f(t)\mathrm{d}t=0\end{array}$，则 $F(x)=\begin{array}{r}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$ 也是以 $T$ 为周期的周期函数。

【注】上面我们提到过，连续的偶函数 $f(x)$ 的原函数中仅有一个原函数是奇函数，这个原函数就是 $F(x)=\begin{array}{r}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$。

---

【补充】复合函数的奇偶性性质

当且仅当内外函数均为奇函数时，复合函数才为奇函数。

即 $f(x)$ 与 $g(x)$ 均为奇函数，则 $f[g(x)]$ 为奇函数。

强化 1

---

设 $F(x)$ 是连续函数 $f(x)$ 的一个原函数，“$M\iff N$” 表示 “ $M$ 的充分必要条件是 $N$ ”，给出以下四个结论：

（1）$F(x)$ 是偶函数 $\iff f(x)$ 是奇函数

（2）$F(x)$ 是奇函数 $\iff f(x)$ 是偶函数

（3）$F(x)$ 是周期函数 $\iff f(x)$ 是周期函数

（4）$F(x)$ 是单调函数 $\iff f(x)$ 是单调函数

其中正确的结论个数为 __________ 。

A． 1

B． 2

C． 3

D． 4

---

【答案】

A

【解析】

对于（1），若 $F(x)$ 为奇函数，则 $f(x)$ 为偶函数；若 $f(x)$ 为奇函数，则 $f(x)$ 的所有原函数均为偶函数，（1）正确。

对于（2），若 $F(x)$ 为偶函数，则 $f(x)$ 为奇函数，但当 $f(x)$ 为偶函数时，$f(x)$ 的原函数中仅有一个是奇函数，（2）错误。

对于（3），若 $F(x)$ 是以 $T$ 为周期的可导函数，则 $f(x)$ 也是以 $T$ 为周期的周期函数，但当 $f(x)$ 为周期函数时，并非所有原函数均为周期函数，（3）错误。

【例】$f(x)=\begin{array}{r}\sin x+1\end{array}$ 是周期函数，但 $F(x)=\begin{array}{r}-\cos x+x\end{array}$ 不是周期函数。

对于（4），若取 $F(x)=\begin{array}{r}{x}^3\end{array}$ 是单增函数，但 $F^{\prime }(x)=f(x)=\begin{array}{r}3x^2\end{array}$ 不是单调函数，（4）错误。

应选 A。

强化 2

---

设 $f(x)$ 连续，则下列函数中必为偶函数的是 __________ 。

A． $\begin{array}{r}{\int }_0^x\frac{{\mathrm{e}}^t-1}{{\mathrm{e}}^t+1}\cdot \ln (t+\sqrt{1+t^2})\mathrm{d}t\end{array}$

B． $\begin{array}{r}{\int }_0^{x}t[f(t)-f(-t)]\mathrm{d}t\end{array}$

C． $\begin{array}{r}{\int }_0^x\mathrm{d}t{\int }_0^t\frac{\arctan u}{1+u^4}\mathrm{d}u\end{array}$

D． $\begin{array}{r}{\int }_1^x\mathrm{d}t{\int }_0^t\frac{{\sin }^{2}u}{1+u^4}\mathrm{d}u\end{array}$

---

【答案】

D

【解析】

强化 3

---

设奇函数 $f(x)$ 在 $(-\mathrm{\infty },+\mathrm{\infty })$ 上有连续导数，$a$ 为任意常数，则 __________ 。

A． $\begin{array}{r}{\int }_0^x[\cos f(t)+f^{\prime }(t)]\mathrm{d}t\end{array}$ 必为奇函数

B． $\begin{array}{r}{\int }_a^x[\cos f(t)+f^{\prime }(t)]\mathrm{d}t\end{array}$ 必为奇函数

C． $\begin{array}{r}{\int }_0^x[\sin f^{\prime }(t)+f(t)]\mathrm{d}t\end{array}$ 必为偶函数

D． $\begin{array}{r}{\int }_a^x[\sin f^{\prime }(t)+f^{\prime }(t)]\mathrm{d}t\end{array}$ 必为奇函数

---

【答案】

A

【解析】

（解析内容待补充）

强化 4

---

设函数 $f(x)=\begin{array}{r}{\int }_0^{\sin x}\sin t^3\mathrm{d}t\end{array},g(x)=\begin{array}{r}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$ ，则 __________ 。

A．$f(x)$ 为奇函数，$g(x)$ 为奇函数

B．$f(x)$ 为奇函数，$g(x)$ 为偶函数

C．$f(x)$ 为偶函数，$g(x)$ 为偶函数

D．$f(x)$ 为偶函数，$g(x)$ 为奇函数

---

【答案】

B

【解析】

（解析内容待补充）

刻意练习

---

设函数 $f(x)$ 在 $(-\mathrm{\infty },+\mathrm{\infty })$ 上有定义，且对于任意的 $x,y$ 恒有 $f(x+y)=f(x)+f(y)$ 。若 $a>0$ ，且 $a\ne 1$ ，则 __________ 。

A． $\begin{array}{r}{\int }_1^x(\frac{1}{a^t-1}+\frac{1}{2})f(t)\mathrm{d}t\end{array}$ 为奇函数

B． $\begin{array}{r}{\int }_1^x(\frac{1}{a^t-1}+\frac{1}{2})f(t)\mathrm{d}t\end{array}$ 为偶函数

C． $\begin{array}{r}{\int }_0^{x}t(\frac{1}{a^t-1}+\frac{1}{2})f(t)\mathrm{d}t\end{array}$ 为奇函数

D． $\begin{array}{r}{\int }_0^{x}t(\frac{1}{a^t-1}+\frac{1}{2})f(t)\mathrm{d}t\end{array}$ 为偶函数

---

【答案】

D

【解析】

（解析内容待补充）

2 无穷小量及其比阶

题型1 无穷小比阶问题

方法一：利用定义法比阶

---

方法二：通过确定无穷小量的等价无穷小来定阶

当 $x\to 0$，若 $f(x)\sim A{x}^k(A\ne 0,k>0)$ ，则 $f(x)$ 为 $x\to 0$ 时 $x$ 的 $k$ 阶无穷小。

---

【注】等价无穷小替换准则总结：

（1）乘除法因式可替换。

（2）不同阶的无穷小量相加减时，可直接替换，取最低阶的那一项。（和取低阶原则）。

（3）同阶的无穷小量相加减，且每一个无穷小量均等价至最简形式（即 $a{x}^k$ 型，其中 $a\ne 0,k>0)$ 不可抵消时，每一项可直接使用等价无穷小替换。

（4）同阶的无穷小量相加减，且每一个无穷小量均等价至最简形式（即 $a{x}^k$ 型，其中 $a\ne 0,k>0)$ 可抵消时，此时需要借助泰勒公式展开。

---

方法三：利用泰勒公式定阶

---

方法四：利用导数定阶法

设 $f(x)$ 为 $x\to 0$ 时的无穷小量，即 $\begin{array}{r}\underset{x\to 0}{lim}f(x)=0\end{array}$ ，有：

（1）若 $f^{\prime }(x)\sim x^k$（ $k$ 为大于 0 的常数），则 $f(x)\sim \begin{array}{r}\frac{1}{k+1}{x}^{k+1}\end{array}$

（2）若 $\begin{array}{r}\underset{x\to 0}{lim}{f}^{\prime }(x)=C\ne 0\end{array}$ ，则 $f(x)\sim Cx$ 。

强化 5

---

当 $x\to 0^{+}$ 时，下列无穷小量中阶数最高的是 __________ 。

A． $\begin{array}{r}\ln \cos x-\sqrt[3]{\cos x}+1\end{array}$

B． $\begin{array}{r}\cos \sqrt{x}\cdot \sqrt{1-\cos \sqrt{x}}\end{array}$

C． $\begin{array}{r}x-\ln (1+x)-\frac{1}{2}x\sin x\end{array}$

D． $\begin{array}{r}x-\ln (1+\sin x)\end{array}$

---

【答案】

D

【解析】

强化 6 （2020 年真题）

---

当 $x\to 0^{+}$ 时，下列无穷小量中阶数最高的是 __________ 。

A． $\begin{array}{r}{\int }_0^x({\mathrm{e}}^{t^2}-1)\mathrm{d}t\end{array}$

B． $\begin{array}{r}{\int }_0^x\ln (1+\sqrt{t^3})\mathrm{d}t\end{array}$

C． $\begin{array}{r}{\int }_0^{\sin x}\sin t^2\mathrm{d}t\end{array}$

D． $\begin{array}{r}{\int }_0^{1-\cos x}\sqrt{{\sin }^{3}t}\mathrm{d}t\end{array}$

---

【答案】

D

【解析】

题型2 乘法中泰勒展开阶数的确定方法

切勿缺项，展开技巧为"头看尾、尾看头"，可参考下列例题。

强化 7

---

试确定常数 $A,B,C$ 的值，使得：

$$\begin{array}{r}{\mathrm{e}}^x(1+Bx+C{x}^2)=1+Ax+o\left(x^3\right),\end{array}$$

其中 $o\left(x^3\right)$ 是当 $x\to 0$ 时比 $x^3$ 高阶的无穷小。

---

【答案】

【解析】

强化 8

---

（2021 年真题）设函数 $f(x)=\begin{array}{r}\frac{\sin x}{1+x^2}\end{array}$ 在 $x=0$ 处的 3 次泰勒多项式为 $ax+b{x}^2+c{x}^3$ ，则 __________ 。

A． $a=1,b=0,c=-\begin{array}{r}\frac{7}{6}\end{array}$

B． $a=1,b=0,c=\begin{array}{r}\frac{7}{6}\end{array}$

C． $a=-1,b=-1,c=-\begin{array}{r}\frac{7}{6}\end{array}$

D． $a=-1,b=-1,c=\begin{array}{r}\frac{7}{6}\end{array}$

---

【答案】

A

【解析】

刻意练习 1

---

当 $x\to 0$ 时，函数 $\begin{array}{r}f(x)={\mathrm{e}}^x\ln (1+x)-x-\frac{1}{2}{x}^2\end{array}$ 与 $\begin{array}{r}g(x)=k(1-\sqrt{\cos x})\ln (x+\sqrt{1+x^2})\end{array}$ 是等价无穷小，则 $k=$ __________ 。

---

【答案】

$\frac{1}{3}$

【解析】

刻意练习 2

---

求极限

$\begin{array}{r}\underset{x\to 0}{lim}\frac{\ln (1+x)\ln (1-x)-\ln (1-x^2)}{x^4}\end{array}$

---

【答案】

$-\frac{1}{12}$

【解析】

3 函数极限计算

题型1 七种未定式的极限计算

函数极限计算是每年考研中的重点，求解的基本思路是：定型-化简-定法，即先判定函数极限的类型，再对函数进行相应的化简，最后再确定极限计算的方法．

---

1. 常见的极限化简方法

（1）非零因子淡化（乘除法中非零项先算出）

（2）加减法中极限存在项可拆出计算

（3）遇到根式想有理化

（4）遇到幂指函数想幂指转换化

---

2．重要的极限求解方法

方法一：等价无穷小替换

方法二：泰勒公式

方法三：洛必达法则

方法四：极限四则运算

方法五：连续的定义

方法六：拉格朗日中值定理

方法七：凑导数定义

方法八：积分中值定理

---

3. 七种未定式极限的常见求解方法

（1）＂$\begin{array}{r}\frac{0}{0}\end{array}$＂型：等价无穷小，泰勒公式，洛必达，四则运算，拉格朗日中值定理

（2）＂$\begin{array}{r}\frac{\mathrm{\infty }}{\mathrm{\infty }}\end{array}$＂型：抓大头，洛必达法则，上下同除最大项

（3）＂$0\cdot \mathrm{\infty }$＂型：转化为＂$\begin{array}{r}\frac{0}{0}\end{array}$＂型或＂$\begin{array}{r}\frac{\mathrm{\infty }}{\mathrm{\infty }}\end{array}$＂型

（4）＂$\mathrm{\infty }-\mathrm{\infty }$＂型：通分，倒代换，提出最大项

（5）＂$1^{\mathrm{\infty }}$＂型：$\begin{array}{r}\underset{x\to ◻}{lim}{u}^v={\mathrm{e}}^{\underset{x\to ◻}{lim}v\cdot (u-1)}\end{array}$

（6）＂${\mathrm{\infty }}^0$＂型 与 ＂$0^0$＂型：$\begin{array}{r}\underset{x\to ◻}{lim}{u}^v={\mathrm{e}}^{\underset{x\to ◻}{lim}v\cdot \ln u}\end{array}$

强化 9

---

求极限：$\begin{array}{r}\underset{x\to 0}{lim}\frac{(1+x{)}^{\frac{2}{x}}-{\mathrm{e}}^2[1+\ln (1+x)]}{x}\end{array}$

---

【答案】

【解析】

强化 10

---

求极限：$\begin{array}{r}\underset{x\to 0}{lim}\frac{1-\cos x\sqrt{\cos 2x}\sqrt[3]{\cos 3x}}{x^2}\end{array}$

---

【答案】

【解析】

刻意练习

---

求极限：$\begin{array}{r}\underset{x\to 0}{lim}\frac{(1+x{)}^x-\cos \frac{x}{2}}{(\sin x-\sin \frac{x}{2})\sin x}\end{array}$

---

【答案】

【解析】

强化 11

---

求极限：$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}\frac{\sqrt{x^2+x+1}[x-\ln ({\mathrm{e}}^x+x)]}{x}\end{array}$

---

【答案】

【解析】

强化 12

---

求极限：$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}(\sqrt[6]{x^6+x^5}-\sqrt[6]{x^6-x^5})\end{array}$

---

【答案】

【解析】

强化 13

---

求极限：$\begin{array}{r}\underset{x\to 0}{lim}{\left(\frac{a_1^x+a_2^x+\cdots +a_n^x}{n}\right)}^{\frac{n}{x}}\end{array}$ ，其中 $a_i>0,i=1,2,3,\cdots ,n$ 。

---

【答案】

【解析】

强化 14

---

设函数 $f(x)$ 在 $x=0$ 的某去心邻域内有定义，且满足：

$\begin{array}{r}\underset{x\to 0}{lim}{[\cos x+\frac{f(x)}{x}]}^{\frac{1}{x^2}}=\mathrm{e}\underset{x\to \mathrm{\infty }}{lim}{(x+\sqrt{1+x^2})}^{\frac{2}{x}}\end{array}$ ，求 $\begin{array}{r}\underset{x\to 0}{lim}\frac{f(x)}{x^3}\end{array}$

---

【答案】

【解析】

强化 15

---

求极限：$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}{(\frac{\pi }{2}-\arctan x)}^{\frac{1}{\ln x}}\end{array}$

---

【答案】

【解析】

强化 16 （2010 年数学三）

---

求极限：$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}{(x^{\frac{1}{x}}-1)}^{\frac{1}{\ln x}}\end{array}$ 。

---

【答案】

【解析】

题型2 涉及变限函数的极限计算

1. 必备基础：变限函数的求导法则

若函数 $f(x)$ 连续，且 $\alpha (x)$, $\beta (x)$ 可导，则：

$$\begin{array}{r}{[{\int }_{\alpha (x)}^{\beta (x)}f(t)\mathrm{d}t]}_x^{\prime }=f[\beta (x)]{\beta }^{\prime }(x)-f[\alpha (x)]{\alpha }^{\prime }(x)\end{array}$$

【注】若变限函数的自变量 $x$ 出现在被积分函数中，即非标准型情形时，应先将自变量 $x$ 设法分离出被积分函数，常用方式有：提出自变量，利用第二类换元法。

---

2. 求解方法

（1）方法一：洛必达法则（首选）

（2）方法二：积分中值定理

若函数 $f(x)$ 在 $[a,b]$ 连续，则存在 $\xi \in (a,b)$ ，使得 $\begin{array}{r}{\int }_a^{b}f(x)\mathrm{d}x=f(\xi )(b-a)\end{array}$ 。

强化 17

---

求极限：$\begin{array}{r}\underset{x\to 0^{+}}{lim}\frac{x\begin{array}{c}{\int }_x^{x^2}\sin (xt)\mathrm{d}t\end{array}}{\begin{array}{c}{\int }_0^{x}t\cdot \sin (x^2-t^2)\mathrm{d}t\end{array}}\end{array}$

---

【答案】

【解析】

强化 18

---

求极限：$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}\frac{\begin{array}{c}{\int }_0^x[t^2({\mathrm{e}}^{\frac{1}{t}}-1)-t]\mathrm{d}t\end{array}}{x^2\ln (1+\begin{array}{c}\frac{1}{x}\end{array})}\end{array}$

---

【答案】

【解析】

强化 19

---

求极限：$\begin{array}{r}\underset{x\to 0}{lim}\frac{\begin{array}{c}{\int }_0^x\mathrm{d}u{\int }_0^{u^2}\arctan (1+t)\mathrm{d}t\end{array}}{x(1-\cos x)}\end{array}$

---

【答案】

【解析】

强化 20 （2021 年数学二）

---

已知函数 $\begin{array}{r}f(t)={\int }_1^{t^2}\mathrm{d}x{\int }_{\sqrt{x}}^t\sin \frac{x}{y}\mathrm{d}y\end{array}$ ，则 $f^{\prime }\left(\begin{array}{r}\frac{\pi }{2}\end{array}\right)=$ __________ 。

---

【答案】

【解析】

题型3 已知极限求其中的待定参数

已知极限结果求其中待定参数的问题，本质还是求函数极限的问题，求解思路仍然是：先定型，再化简，后定法。

---

【注】常用的几个重要结论：

（1）若 $limf(x)g(x)=A$（存在），且 $limf(x)=\mathrm{\infty }$ ，则 $limg(x)=0$ ；

（2）若 $lim\begin{array}{r}\frac{f(x)}{g(x)}\end{array}=A$ ，且 $limg(x)=0$ ，则 $limf(x)=0$ ；

（3）若 $lim\begin{array}{r}\frac{f(x)}{g(x)}\end{array}=A\ne 0$ ，且 $limf(x)=0$ ，则 $limg(x)=0$ 。

强化 21

---

已知 $\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}{\mathrm{e}}^x[{\int }_0^{\sqrt{x}}{\mathrm{e}}^{-t^2}\mathrm{d}t+a]=b\end{array}$ ，求常数 $a,b$ 。

---

【答案】

$a = -\frac{\sqrt{\pi}}{2},\quad b = \frac{1}{2}$

【解析】

解析内容

强化 22

---

已知 $\begin{array}{r}\underset{x\to 0}{lim}\frac{2\arctan x-\ln \begin{array}{c}\frac{1+x}{1-x}\end{array}}{x^n}=c\end{array}$ ，且 $c\ne 0$ ，求常数 $n,c$ 。

---

【答案】

$n = 3,\quad c = -\frac{2}{3}$

【解析】

解析内容

强化 23

---

已知 $\begin{array}{r}lim(\sqrt{x^2+x+1}-(ax+b))=0\end{array}$ ，求常数 $a,b$ 。

---

【答案】

【解析】

解析内容

刻意练习

---

设 $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}(\sqrt[3]{x^3-1}+ax+b)=0\end{array}$ ，求常数 $a,b$ 。

---

【答案】

$a = -1,\quad b = 0$

【解析】

解析内容

题型4 需要分左右求函数极限

1. 基本内容

（1） $\begin{array}{r}\underset{x\to x_0}{lim}f(x)=a\iff \underset{x\to x_0^{+}}{lim}f(x)=\underset{x\to x_0^{-}}{lim}f(x)=a\end{array}$ 。

（2） $\begin{array}{r}\underset{x\to \mathrm{\infty }}{lim}f(x)=a\iff \underset{x\to +\mathrm{\infty }}{lim}f(x)=\underset{x\to -\mathrm{\infty }}{lim}f(x)=a\end{array}$ 。

---

2. 常见的需要分左右极限的情形

（1） ${\mathrm{e}}^{\mathrm{\infty }}$ 型

当 $x\to 0$ 时， $\begin{array}{r}\underset{x\to 0^{+}}{lim}{\mathrm{e}}^{\frac{1}{x}}=+\mathrm{\infty }\end{array}$, $\begin{array}{r}\underset{x\to 0^{-}}{lim}{\mathrm{e}}^{\frac{1}{x}}=0\end{array}$ 。

（2） $\arctan \mathrm{\infty }$ 型

当 $x\to 0$ 时， $\begin{array}{r}\underset{x\to 0^{+}}{lim}\arctan \frac{1}{x}=\frac{\pi }{2}\end{array}$, $\begin{array}{r}\underset{x\to 0^{-}}{lim}\arctan \frac{1}{x}=-\frac{\pi }{2}\end{array}$ 。

（3）$|f(x)|$ 型，其中 $f(x)\to 0$ 或 $f(x)\to \mathrm{\infty }$

当 $x\to 0^{+}$ 时，$|x|=x$ ；当 $x\to 0^{-}$ 时，$|x|=-x$ 。

（4）取整函数 $[x]$ 在整数点处的极限

当 $x\to 0^{+}$ 时，$[x]=0$ ；当 $x\to 0^{-}$ 时，$[x]=-1$ 。

（5）求分段函数在分段点处的极限，且分段函数在分段点两侧的函数表达式不同。

强化 24

---

求 $\begin{array}{r}\underset{x\to 0}{lim}(\frac{\ln (1+{\mathrm{e}}^{\frac{2}{x}})}{\ln (1+{\mathrm{e}}^{\frac{1}{x}})}-2[x])\end{array}$ ，其中 $[x]$ 为取整函数。

---

【答案】

【解析】

4 函数极限的定义与性质

题型1 函数极限定义的理解

【考】函数极限定义的理解

$$\underset{x\to x_0}{lim}f(x)=A\iff \mathrm{\forall }\epsilon >0,\mathrm{\exists }\delta >0，\mathrm{当}0<|x-x_0|<\delta \mathrm{时}，\mathrm{有}|f(x)-A|<\epsilon$$

---

【注1】极限 $\begin{array}{r}\underset{x\to x_0}{lim}\end{array}f(x)$ 与 $f(x)$ 在 $x_0$ 处的函数值无关。

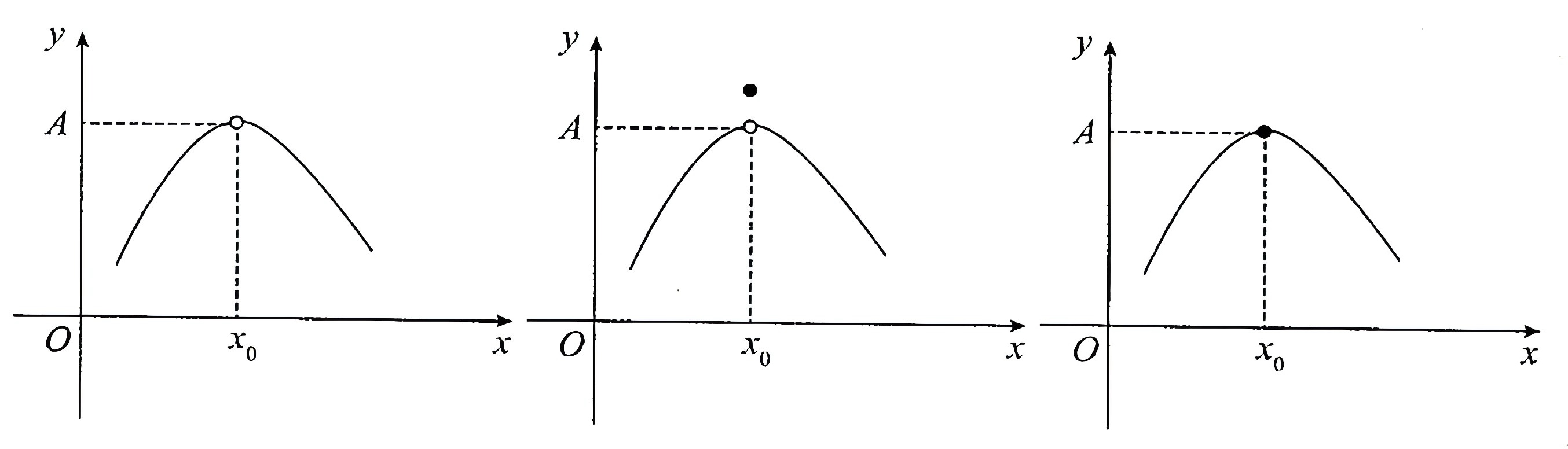
如图所示，三幅图中极限 $\begin{array}{r}\underset{x\to x_0}{lim}\end{array}f(x)$ 均等于 $A$ ，但是函数值 $f\left(x_0\right)$ 却可以不存在，也可以存在，且存在时 $f\left(x_0\right)$ 可以等于 $A$ ，也可以不等于 $A$ ，所以极限 $\begin{array}{r}\underset{x\to x_0}{lim}\end{array}f(x)$ 结果与该点函数值没有任何关系。

假如 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)=f\left(x_0\right)\end{array}$ 时（最右），函数 $f(x)$ 在 $x_0$ 处连续。

---

【注2】若极限 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)\end{array}$ 存在，则函数 $f(x)$ 在 $x=x_0$ 的某去心邻域内处处有定义。

---

【注3】若极限 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)\end{array}$ 存在，则极限 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)\end{array}$ 是一个数。

---

【注4】存在的函数极限与无穷小量之间的关系定理

若 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)=A\end{array}$ ，则 $f(x)=A+\alpha (x)$ ，其中 $\begin{array}{r}\underset{x\to x_0}{lim}\alpha (x)=0\end{array}$

强化 25

---

设 $\begin{array}{r}\underset{x\to 0^{+}}{lim}f(x)\end{array}$ 存在，且函数满足 $\begin{array}{r}f(x)=\frac{1}{x}-\frac{1-\pi x}{\arctan x}+2{(1+\frac{1}{x})}^x\underset{x\to 0^{+}}{lim}f(x)\end{array}$ ，则 $\begin{array}{r}\underset{x\to 0^{+}}{lim}f(x)=\end{array}$ __________ 。

---

【答案】

【解析】

强化 26

---

设 $\begin{array}{r}\underset{x\to 0}{lim}[\frac{f(x)-1}{\tan x}-\frac{{\mathrm{e}}^x\sin x}{{\tan }^{2}x}]=2\end{array}$ ，则 $\begin{array}{r}\underset{x\to 0}{lim}f(x)=\end{array}$ __________ 。

---

【答案】

【解析】

题型2 函数极限的局部保号性

1. 已知函数极限的正负性，欲知被求极限函数的正负性，立即想到“保号性”，这一问题在极值与拐点问题中应用较多。

---

2. 比较两函数在某一个趋向下的大小，立即想到“保号性”。

（1）若 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)>\underset{x\to x_0}{lim}g(x)\end{array}$ ，则在 $x_0$ 的某去心邻域内 $f(x)>g(x)$

（2）若 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)<\underset{x\to x_0}{lim}g(x)\end{array}$ ，则在 $x_0$ 的某去心邻域内 $f(x)<g(x)$

强化 27

---

设 $f(x)={\ln }^{10}x$, $g(x)=x$, $h(x)={\mathrm{e}}^{\frac{x}{10}}$ ，则当 $x$ 充分大时有 __________ 。

A．$g(x)<h(x)<f(x)$

B．$h(x)<g(x)<f(x)$

C．$f(x)<g(x)<h(x)$

D．$g(x)<f(x)<h(x)$

---

【答案】

C

【解析】

当 $x$ 充分大时，比较三个函数的增长趋势。

由于 $f(x)={\ln }^{10}x$ 是对数函数的高次幂，$g(x)=x$ 是线性函数，$h(x)={\mathrm{e}}^{\frac{x}{10}}$ 是指数函数。

指数函数增长最快，线性函数次之，对数函数增长最慢，因此有 $f(x)<g(x)<h(x)$。

应选 C。

题型3 函数的有界性

1. 利用有界性的定义

---

2. 利用连续函数的有界定理

（1）若 $f(x)$ 在闭区间 $[a,b]$ 上连续，则 $f(x)$ 在 $[a,b]$ 上有界。

（2）若 $f(x)$ 在开区间 $(a,b)$ 上连续，且极限 $\begin{array}{r}\underset{x\to a^{+}}{lim}f(x)\end{array}$ 与 $\begin{array}{r}\underset{x\to b^{-}}{lim}f(x)\end{array}$ 都存在，则 $f(x)$ 在 $(a,b)$ 上有界。

（3）若 $f(x)$ 在 $[a,b)$ 上连续，且极限 $\begin{array}{r}\underset{x\to a^{+}}{lim}f(x)\end{array}$ 存在，则 $f(x)$ 在 $[a,b)$ 上有界。

（4）若 $f(x)$ 在 $(-\mathrm{\infty },+\mathrm{\infty })$ 上连续，且极限 $\begin{array}{r}\underset{x\to -\mathrm{\infty }}{lim}f(x)\end{array}$ 与 $\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}f(x)\end{array}$ 都存在，则 $f(x)$ 在 $(-\mathrm{\infty },+\mathrm{\infty })$ 上有界。

---

3. 初等函数有界区间的求解步骤

步骤 1：求初等函数的无定义点，确定定义区间。根据初等函数在其定义区间上处处连续，确定出函数的连续区间。

步骤 2：利用连续函数的有界定理，确定有界区间。

【注】需要注意的是，当 $\begin{array}{r}\underset{x\to ◻}{lim}f(x)\end{array}$ 不存在（且不为 $\mathrm{\infty }$）时，$f(x)$ 在 $x\to ◻$ 时可能有界，也可能无界，例如：$y=\begin{array}{r}\sin \frac{1}{x}\end{array}$ 在 $x\to 0$ 时有界，$y=\begin{array}{r}\frac{1}{x}\sin \frac{1}{x}\end{array}$ 在 $x\to 0$ 时无界。

强化 28

---

已知函数 $f(x)=\begin{array}{r}\frac{(x^3-1)\sin x}{(x^2+1)x}\end{array}$, $g(x)=\begin{array}{r}\frac{1}{x}\sin \frac{1}{x}\end{array}$ ，则在其定义域内 __________ 。

A．$f(x)$ 有界，$g(x)$ 有界

B．$f(x)$ 有界，$g(x)$ 无界

C．$f(x)$ 无界，$g(x)$ 有界

D．$f(x)$ 无界，$g(x)$ 无界

---

【答案】

B

【解析】

解析内容占位

强化 29

---

以下四个命题中，正确的是 __________ ．

A．若 $f^{\prime }(x)$ 在 $(0,1)$ 内连续，则 $f(x)$ 在 $(0,1)$ 内有界

B．若 $f(x)$ 在 $(0,1)$ 内连续，则 $f(x)$ 在 $(0,1)$ 内有界

C．若 $f^{\prime }(x)$ 在 $(0,1)$ 内有界，则 $f(x)$ 在 $(0,1)$ 内有界

D．若 $f(x)$ 在 $(0,1)$ 内有界，则 $f^{\prime }(x)$ 在 $(0,1)$ 内有界

---

【答案】

C

【解析】

解析内容占位

强化 30

---

已知函数 $\begin{array}{r}f(x)=\frac{\begin{array}{c}{\int }_0^x\ln (1+t^2)\mathrm{d}t\end{array}}{x^{\alpha }}\end{array}$ 在 $(0,+\mathrm{\infty })$ 上有界，则 $\alpha$ 取值范围为 __________ ．

A．$(0,3)$

B．$(0,3]$

C．$(1,3)$

D．$(1,3]$

---

【答案】

D

【解析】

解析内容占位

5 数列极限的定义与性质

题型1 数列极限的定义与性质

强化 31

---

“对任意给定的 $\epsilon \in (0,1)$ ，总存在正整数 $N$ ，当 $n⩾N$ 时，恒有 $|x_n-a|⩽2\epsilon$” 是 “数列 $\left\{x_n\right\}$ 收敛于 $a$” 的 __________ ．

A．充分必要条件

B．充分非必要条件

C．必要非充分条件

D．既非充分也非必要条件

---

【答案】

A

【解析】

解析内容占位

强化 32

---

已知 $a_n=\begin{array}{r}\sqrt[n]{n}\end{array}-\begin{array}{r}\frac{(-1{)}^n}{n}\end{array}$ $(n=1,2,\cdots )$ ，则 $\left\{a_n\right\}$ __________ ．

A．有最大值，有最小值

B．有最大值，没有最小值

C．没有最大值，有最小值

D．没有最大值，没有最小值

---

【答案】

C

【解析】

解析内容占位

强化 33

---

设 $\left\{x_n\right\}$ 是数列，则 “ $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\frac{x_{n+1}}{x_n}=1\end{array}$” 是 “ $\left\{x_n\right\}$ 收敛” 的 __________ ．

A．充分必要条件

B．充分非必要条件

C．必要非充分条件

D．既非充分也非必要条件

---

【答案】

D

【解析】

解析内容占位

强化 34

---

设 $\left\{x_n\right\}$ 是数列，且 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_{3n}\end{array}=\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_{3n+1}\end{array}=1$ ，则 $\left\{x_n\right\}$ 收敛的充分条件为 __________ 。

A．$x_{3n+2}=\begin{array}{r}{\left(\frac{\sqrt[n]{2}+\sqrt[n]{3}}{2}\right)}^n\end{array}$

B．$x_{3n+2}=\begin{array}{r}(\sqrt{n^2+2n}-\sqrt{n^2-2n})\end{array}$

C．$x_{3n+2}=\begin{array}{r}n\cdot \sqrt[n]{n}\cdot (\sqrt[n]{2}-1)\end{array}$

D．$x_{3n+2}=\begin{array}{r}\sum _{k=1}^n\frac{1}{k(k+1)}\end{array}$

---

【答案】

D

【解析】

解析内容占位

强化 35

---

设数列 $\left\{x_n\right\}$ 与 $\left\{y_n\right\}$ 满足 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n{y}_n=0\end{array}$ ，则下列断言正确的是 __________ ．

A．若 $\left\{x_n\right\}$ 发散，则 $\left\{y_n\right\}$ 发散

B．若 $\left\{x_n\right\}$ 无界，则 $\left\{y_n\right\}$ 必有界

C．若 $\left\{x_n\right\}$ 有界，则 $\left\{y_n\right\}$ 必为无穷小

D．若 $\left\{\begin{array}{r}\frac{1}{x_n}\end{array}\right\}$ 为无穷小，则 $\left\{y_n\right\}$ 必为有界

---

【答案】

C

【解析】

解析内容占位

题型2 复合型数列 $\{f(x_n)\}$ 与 数列 $\{x_n\}$ 之间的敛散性关系

性质 1：

设函数 $f(x)$ 在区间 $(a,b)$ 上连续，若数列 $\left\{x_n\right\}$ 收敛于 $(a,b)$ 内一点 $A$ ，则:

数列 $\left\{f\left(x_n\right)\right\}$ 收敛于 $f(A)$ ，即：

“若 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n=A\end{array}$ ，则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}f\left(x_n\right)=f(A)\end{array}$”

---

性质 2：

设函数 $f(x)$ 在区间 $(a,b)$ 上单调连续，若数列 $\left\{f\left(x_n\right)\right\}$ 收敛于 $f(x)$ 值域内一点 $f(A)$ ，则数列 $\left\{x_n\right\}$ 收敛于 $A$ ，即：

“若 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}f\left(x_n\right)=f(A)\end{array}$ ，则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n=A\end{array}$”

---

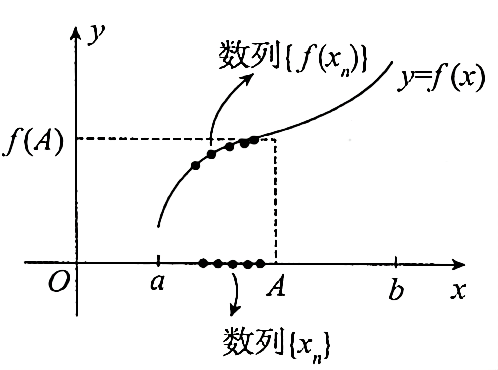
【注】需注意以下几点：

（1）设函数 $f(x)$ 在区间 $(a,b)$ 上连续但不单调，若数列 $\left\{f\left(x_n\right)\right\}$ 收敛于 $f(x)$ 值域内一点 $f(A)$ ，但数列 $\left\{x_n\right\}$ 不一定收敛。

（2）设函数 $f(x)$ 在区间 $(a,b)$ 上单调，若数列 $\left\{x_n\right\}$ 收敛于 $(a,b)$ 内一点 $x_0$ ，但数列 $\left\{f\left(x_n\right)\right\}$ 未必收敛。

（3）设函数 $f(x)$ 单调，若数列 $\left\{f\left(x_n\right)\right\}$ 收敛，但数列 $\left\{x_n\right\}$ 未必收敛。

强化 36

---

设实数数列 $\left\{a_n\right\}$ ，给出以下四个命题：

（1）若 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{a}_n=A\end{array}$ ，则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\sin a_n=\sin A\end{array}$ 。

（2）若 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\sin a_n=\sin A\end{array}$ ，则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{a}_n=A\end{array}$ 。

（3）若 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{a}_n=A\end{array}$ ，则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{\mathrm{e}}^{a_n}={\mathrm{e}}^A\end{array}$ 。

（4）若 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{\mathrm{e}}^{a_n}={\mathrm{e}}^A\end{array}$ ，则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{a}_n=A\end{array}$ 。

其中真命题的个数是 __________ ．

A． 1

B． 2

C． 3

D． 4

---

【答案】

B

【解析】

解析内容占位

强化 37

---

（2022 年真题）已知数列 $\left\{x_n\right\}$ ，其中 $-\begin{array}{r}\frac{\pi }{2}\end{array}⩽x_n⩽\begin{array}{r}\frac{\pi }{2}\end{array}$ ，则 __________ ．

A．当 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\cos (\sin x_n)\end{array}$ 存在时，$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}$ 存在

B．当 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\sin (\cos x_n)\end{array}$ 存在时，$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}$ 存在

C．当 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\cos (\sin x_n)\end{array}$ 存在时，$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\sin x_n\end{array}$ 存在，但 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}$ 不一定存在

D．当 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\sin (\cos x_n)\end{array}$ 存在时，$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\cos x_n\end{array}$ 存在，但 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}$ 不一定存在

---

【答案】

D

【解析】

解析内容占位

强化 38

---

（2024 年真题）已知数列 $\left\{a_n\right\}(a_n\ne 0)$ ，若 $\left\{a_n\right\}$ 发散，则 __________ ．

A．$\{a_n+\begin{array}{r}\frac{1}{a_n}\end{array}\}$ 发散

B．$\{a_n-\begin{array}{r}\frac{1}{a_n}\end{array}\}$ 发散

C．$\{{\mathrm{e}}^{a_n}+\begin{array}{r}\frac{1}{{\mathrm{e}}^{a_n}}\end{array}\}$ 发散

D．$\{{\mathrm{e}}^{a_n}-\begin{array}{r}\frac{1}{{\mathrm{e}}^{a_n}}\end{array}\}$ 发散

---

【答案】

C

【解析】

解析内容占位

6 数列极限计算

题型1 数列极限的通项已知，且为未定式极限

【考】归结原则（海涅定理）

函数极限 $\begin{array}{r}\underset{x\to x_0}{lim}f(x)=A\end{array}$ 的充分必要条件是，对于任一收敛于 $x_0$ 的数列 $\left\{x_n\right\}$ ，且 $x_n\ne x_0$ ，其所对应的数列 $f\left(x_n\right)$ ，有 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}f\left(x_n\right)=A\end{array}$ 。

---

【注】利用归结原则，可将数列极限转化为函数极限处理，其原理为：

$$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}f(x)=A\Rightarrow \underset{n\to \mathrm{\infty }}{lim}f(n)=A\end{array}$$

强化 39

---

求极限 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{n}^2(\arctan \frac{a}{n}-\arctan \frac{a}{n+1})\end{array}$ ，其中参数 $a\ne 0$ 。

---

【答案】

$a$

【解析】

解析内容占位

题型2 $n$ 项和式数列极限

1. 利用定积分定义（分割、近似、求和、取极限）

（1）一般形式

• 右端点：$\begin{array}{r}{\int }_a^{b}f(x)\mathrm{d}x=\underset{n\to \mathrm{\infty }}{lim}\sum _{k=1}^{n}f[a+\frac{k}{n}(b-a)]\cdot \frac{b-a}{n}\end{array}$

• 左端点：$\begin{array}{r}{\int }_a^{b}f(x)\mathrm{d}x=\underset{n\to \mathrm{\infty }}{lim}\sum _{k=1}^{n}f[a+\frac{k-1}{n}(b-a)]\cdot \frac{b-a}{n}\end{array}$

（2）特殊形式（考查 $[0,1]$ 的区间）

• 右端点：$\begin{array}{r}{\int }_0^{1}f(x)\mathrm{d}x=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}\sum _{k=1}^{n}f\left(\frac{k}{n}\right)\end{array}$

• 左端点：$\begin{array}{r}{\int }_0^{1}f(x)\mathrm{d}x=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}\sum _{k=1}^{n}f\left(\frac{k-1}{n}\right)\end{array}$

• 中点：$\begin{array}{r}{\int }_0^{1}f(x)\mathrm{d}x=\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}\sum _{k=1}^{n}f\left(\frac{2k-1}{2n}\right)\end{array}$

---

2. 利用夹逼准则

若存在 $N>0$ ，当 $n>N$ 时，满足

（1）$y_n⩽x_n⩽z_n$ ，

（2）$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{y}_n=a\end{array}$ 且 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{z}_n=a\end{array}$ ，

则数列 $\left\{x_n\right\}$ 极限存在，且 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n=a\end{array}$ 。

强化 40 （基础题）

---

（I）求 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}[\ln (1+\frac{1}{n})+\ln (1+\frac{2}{n})+\cdots +\ln (1+\frac{n}{n})]\end{array}$ 。

（II）求 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}[\ln (1+\frac{1}{n})+\ln (1+\frac{2}{n})+\cdots +\ln (1+\frac{2n}{n})]\end{array}$ 。

---

【答案】

$\begin{aligned}\int_{0}^{1} \ln(1+x) \mathrm{d}x = 2\ln2 - 1\end{aligned}$

【解析】

解析内容占位

强化 41

---

求极限 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}[\frac{\sin \begin{array}{c}\frac{\pi }{n}\end{array}}{n+1}+\frac{\sin \begin{array}{c}\frac{2\pi }{n}\end{array}}{n+\begin{array}{c}\frac{1}{2}\end{array}}+\cdots +\frac{\sin \pi }{n+\begin{array}{c}\frac{1}{n}\end{array}}]\end{array}$ 。

---

【答案】

$\begin{aligned}\frac{2}{\pi}\end{aligned}$

【解析】

解析内容占位

题型3 $n$ 项积式数列极限

取对数（将 $n$ 项积问题转化为 $n$ 项和问题），再利用题型 2 的求解方法进行处理。

强化 42

---

求极限 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\sqrt[n]{(1+\frac{1}{n^2})\cdot (1+\frac{2^2}{n^2})\cdots (1+\frac{n^2}{n^2})}\end{array}$ 。

---

【答案】

$1$

【解析】

解析内容占位

刻意练习

---

极限 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\frac{\sqrt[n]{n!}}{n}\end{array}=$ __________ 。

---

【答案】

$\begin{aligned}\frac{1}{e}\end{aligned}$

【解析】

解析内容占位

题型4 利用夹逼准则求数列极限

定理 若存在 $N>0$ ，当 $n>N$ 时，满足：

（1）$y_n⩽x_n⩽z_n$ ，

（2） $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{y}_n=\underset{n\to \mathrm{\infty }}{lim}{z}_n=a\end{array}$ ， 则 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n=a\end{array}$ 。

---

【注】上式中（2）若改为 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}(z_n-y_n)=0\end{array}$ ，则无法确定 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}$ 的存在性。

强化 44

---

设周期为 1 的周期函数 $f(x)=x-[x]$ （$[x]$ 表示不超过 $x$ 的最大整数）。

（I）当 $n⩽x<n+1$ （$n$ 为正整数）时，证明：$\begin{array}{r}\frac{n}{2}⩽{\int }_0^{x}f(t)\mathrm{d}t<\frac{n+1}{2}\end{array}$

（II）求 $\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}\frac{1}{x}{\int }_0^{x}f(t)\mathrm{d}t\end{array}$ 。

---

【答案】

（I）证明略；（II）$\begin{aligned}\frac{1}{2}\end{aligned}$

【解析】

解析内容占位

刻意练习

---

设函数 $f(x)$ 为非负且以 $T$ 为周期的连续周期函数，证明：

$$\begin{array}{r}\underset{x\to +\mathrm{\infty }}{lim}\frac{\begin{array}{c}{\int }_0^{x}f(t)\mathrm{d}t\end{array}}{x}=\frac{1}{T}{\int }_0^{T}f(t)\mathrm{d}t\end{array}$$

---

【答案】

证明略

【解析】

解析内容占位

题型5 利用单调有界准则求数列极限

1. 单调有界准则的内容

（1）单调增且有上界的数列必有极限；

（2）单调减且有下界的数列必有极限。

---

2. 常考题型及求解方法

（1）考题形式：

已知数列 $\left\{x_n\right\}$ 有递推公式 $x_{n+1}=f\left(x_n\right)$ ，证明 $\left\{x_n\right\}$ 极限存在并求极限。

该问题通常利用单调有界准则求解，即先证明该数列单调增加有上界（或单调减小有下界），可知极限 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}=A$ 存在，再对递推公式两边同取极限，得到极限值 $A$ 满足的方程，解方程即可求得极限结果。

但是，在实际问题求解中，单调性和有界性的判定是一大难点，这里总结了单调性和有界性的常用解法。

（2）有界性证明

常用方法：先求极限再用数学归纳法证明；利用重点不等式放缩，常见的不等式有：

（1） ${\mathrm{e}}^x-1⩾x(x\in R)$ ，当且仅当 $x=0$ 时取等号；

（2）$x⩾\ln (1+x)(x>-1)$ ，当且仅当 $x=0$ 时取等号；

（3）当 $0<x<\begin{array}{r}\frac{\pi }{2}\end{array}$ 时， $\tan x>x>\sin x$ ；

（4）当 $x>0$ 时，$x>\sin x$ ；

（5）当 $x>0$ 时，$\begin{array}{r}\frac{1}{x+1}\end{array}<\ln (1+\begin{array}{r}\frac{1}{x}\end{array})<\begin{array}{r}\frac{1}{x}\end{array}$ ；

（6）当 $x>0$ 时，$\begin{array}{r}\frac{x}{x+1}\end{array}<\ln (1+x)<x$。

（3）单调性证明

法一：作差与 0 比

法二：作比 与 1比

法三：利用导数判定单调性

已知 $x_{n+1}=f\left(x_n\right)$ ，则：

（1）若 $f^{\prime }(x)>0$ ，

当 $x_1<x_2$ 时，$\left\{x_n\right\}$ 单调递增；当 $x_1>x_2$ 时，$\left\{x_n\right\}$ 单调递减。

（2）若 $f^{\prime }(x)<0$ 时，$\left\{x_n\right\}$ 无单调性。

---

3. 柯西收敛准则

若数列无单调性时，将无法利用“单调有界准则”证明极限存在，此时可使用柯西收敛准则的方法，即证明 $|x_n-A|\to 0(n\to \mathrm{\infty })$ ，具体如下：

• 题设：已知 $x_{n+1}=f\left(x_n\right)$ ，证明 $\left\{x_n\right\}$ 极限存在，并求极限。

• 核心：柯西收敛准则的核心在于求解出 $|f^{\prime }(\xi )|⩽k<1$。

• 步骤：设 $\underset{n\to \mathrm{\infty }}{lim}{x}_n=A$ ，则 $A=f(A)$ ，于是

$$\begin{array}{rl}|x_n-A|& =|f\left(x_{n-1}\right)-f(A)|\\ & =|f^{\prime }(\xi )||x_{n-1}-A|\\ & ⩽k|x_{n-1}-A|\\ & ⩽k^2|x_{n-2}-A|\\ & ⩽\cdots ⩽k^{n-1}|x_1-A|\to 0(n\to \mathrm{\infty })\end{array}$$

强化 45

---

设数列 $\left\{x_n\right\}$ 满足：$x_1>0,x_n{\mathrm{e}}^{x_{n+1}}={\mathrm{e}}^{x_n}-1$ （$n=1,2,\cdots$）。试证明 $\left\{x_n\right\}$ 收敛，并求 $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}_n\end{array}$ 。

---

【答案】

$\begin{aligned}\lim _{n \rightarrow \infty} x_{n} = 0\end{aligned}$

【解析】

解析内容占位

强化 46

---

设 $x_1=1,x_{n+1}=\begin{array}{r}\frac{1+2x_n}{1+x_n}\end{array}$ （$n=1,2,\cdots$），试证数列 $\left\{x_n\right\}$ 极限存在，并求此极限。

---

【答案】

$\begin{aligned}\lim _{n \rightarrow \infty} x_{n} = \sqrt{2}\end{aligned}$

【解析】

解析内容占位

7 连续与间断

题型1 函数的连续与间断的断定

1．连续的判定方法

（1）方法一：初等函数在其有定义的区间上连续。

（2）方法二：利用连续的定义

• 不需分左右极限时：$\begin{array}{r}\underset{x\to x_0}{lim}f(x)=f\left(x_0\right)\end{array}$；

• 需要分左右极限时：$\begin{array}{r}\underset{x\to x_0^{-}}{lim}f(x)=\underset{x\to x_0^{+}}{lim}f(x)=f\left(x_0\right)\end{array}$。

---

【注】函数 $f(x)$ 在点 $x_0$ 处连续必须同时满足以下三个条件：

• $f(x)$ 在 $U(x_0,\delta )$ 内有定义；

• 极限 $\begin{array}{r}\underset{x\to x_0}{lim}\end{array}f(x)$ 存在；

• $\begin{array}{r}\underset{x\to x_0}{lim}\end{array}f(x)=f\left(x_0\right)$。

---

2．连续函数的保号性（可根据图像理解）

设 $f(x)$ 在 $x=x_0$ 处连续，

（1）若 $f\left(x_0\right)>0$，则在 $x_0$ 的某邻域内 $f(x)>0$；

（2）若 $f\left(x_0\right)<0$，则在 $x_0$ 的某邻域内 $f(x)<0$。

---

3．一个易错点

若 $f(x)$ 在 $x=x_0$ 处连续，则在 $x=x_0$ 的某个邻域内 $f(x)$ 也连续，注意！这句话是错误的。

【分析】狄利克雷函数

$$D(x)=\{\begin{array}{ll}1,& x\text{ 为有理数，}\\ 0,& x\text{ 为无理数。}\end{array}$$

取函数 $f(x)=x\cdot D(x)$，该函数在 $x=0$ 处连续，但在 $x=0$ 的任一邻域内均不连续。

显然，可以得出关于可导性的类似结论：若 $f(x)$ 在 $x=x_0$ 处可导，无法推出在 $x=x_0$ 的某个邻域内 $f(x)$ 也可导。

---

4．间断点分类

• 第一类间断点：$\begin{array}{r}\underset{x\to x_0^{-}}{lim}\end{array}f(x)$ 与 $\begin{array}{r}\underset{x\to x_0^{+}}{lim}\end{array}f(x)$ 均存在。

  • 可去间断点：$\begin{array}{r}\underset{x\to x_0}{lim}\end{array}f(x)\ne f\left(x_0\right)$；

  • 跳跃间断点：$\begin{array}{r}\underset{x\to x_0^{-}}{lim}\end{array}f(x)\ne \begin{array}{r}\underset{x\to x_0^{+}}{lim}\end{array}f(x)$。

• 第二类间断点：$\begin{array}{r}\underset{x\to x_0^{-}}{lim}\end{array}f(x)$ 与 $\begin{array}{r}\underset{x\to x_0^{+}}{lim}\end{array}f(x)$ 至少有一个不存在。

  • 无穷间断点：$\begin{array}{r}\underset{x\to x_0^{-}}{lim}\end{array}f(x)$、$\begin{array}{r}\underset{x\to x_0^{+}}{lim}\end{array}f(x)$ 至少有一个是 $\mathrm{\infty }$；

  • 振荡间断点：$\begin{array}{r}\underset{x\to x_0^{-}}{lim}\end{array}f(x)$、$\begin{array}{r}\underset{x\to x_0^{+}}{lim}\end{array}f(x)$ 至少有一个是振荡的不存在。

---

5．间断点判定

（1）找出函数的无定义点，及分段函数的分段点。

（2）分别求这些点处的极限，并作出判定。

题型2 涉及极限式函数的问题

1. 常见的极限式函数

$$F(x)=\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}f(n,x)\end{array},F(x)=\begin{array}{r}\underset{t\to t_0}{lim}f(x,t)\end{array}$$

【注】涉及极限式函数的问题，一般先求极限，确定具体的函数。

---

2. 常用结论

（1）

$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{q}^n=\{\begin{array}{ll}\mathrm{\infty },& |q|>1\\ 0,& |q|<1\\ 1,& q=1\\ \text{ 不存在，}& q=-1\end{array}\end{array}$

$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{x}^n=\{\begin{array}{ll}\mathrm{\infty },& |x|>1\\ 0,& |x|<1\\ 1,& x=1\\ \text{ 不存在, }& x=-1\end{array}\end{array}$

（2） $\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}{\mathrm{e}}^{nx}=\{\begin{array}{ll}+\mathrm{\infty },& x>0\\ 1,& x=0\\ 0,& x<0\end{array}\end{array}$

题型3 连续函数的性质

1. 四则运算性质

设函数 $f(x)$, $g(x)$ 在点 $x_0$ 处连续，则：

$$\begin{array}{r}f(x)\pm g(x)\end{array},\begin{array}{r}f(x)\cdot g(x)\end{array},\begin{array}{r}\frac{f(x)}{g(x)}\end{array}[g\left(x_0\right)\ne 0]$$

在点 $x_0$ 处也连续。

---

2. 复合函数的连续性

设函数 $y=f[g(x)]$ 是由函数 $y=f(u)$ 与 $u=g(x)$ 复合而成，若 $u=g(x)$ 在 $x=x_0$ 处连续，且 $g\left(x_0\right)=u_0$，而 $y=f(u)$ 在 $u=u_0$ 处连续，则复合函数 $y=f[g(x)]$ 在 $x=x_0$ 处连续。

---

3. 反函数的连续性

设有函数 $y=f(x),x\in D$。如果函数 $f(x)$ 是在 $D$ 上单调增加（或单调减少）的连续函数，则它的反函数 $x=f^{-1}(y)$ 在 $D_{f^{-1}}$ 上也是单调增加（或减少）的连续函数，其中 $D_{f^{-1}}=\{y\mid y=f(x),x\in D\}$。